戻る
50年をかえりみる

Fermi面効果

近藤 淳*

§1.　はじめに

金属の自由電子はFermi球を形作っているが，それは安定なおとなしい性質のもので，その表面（Fermi面）には多少の変化が起こっても，それは全体として小さな摂動と考えられてきた．しかし，金属電子は時に特異に振舞うことがあり，不安定性を示すこともある．多くの場合，これらの振舞はFermi面という境界面の存在に関係しており，そのうちのあるものをFermi面効果と呼んでいる．1)これは金属中の磁性不純物の問題に始まった**が，そのほかにも2, 3の関連した現象があり，それらを歴史的に眺めてみるのがこの稿の目的である．

§2.　s-d相互作用

3d遷移金属元素の強磁性の起源についてZenerは次のようなモデルを考えた．2)まず3d電子は各原子に局在して動けないが，そのスピンは自由に向きを変えることができ，

それと自由に動ける4s電子のスピンとの間に交換相互作用 J が働く．もし3d電子のスピンが揃って磁化 M を持ったとすると，4s電子には磁場 JM が働き，cを4s電子のPauli帯磁率として−(1/2)c(JM)2だけのエネルギーの下がりがある．これは M が最大（強磁性）のときもっとも安定となる．糟谷3)はこの議論をさらに進め，3dと4s間の交換相互作用にスピンの非対角項と4s電子の波数q≠0の散乱も含めてsd相互作用と呼び，これを2次摂動で消去して二つの3dスピンの間の交換相互作用を導いた．その大きさは3dスピン間の距離Rの複雑な関数である．そのため，この交換相互作用を最小にする3dスピン配列は強磁性とは限らない．また糟谷4)は3dスピン（一般に局在スピン）がランダムに向いているとき4s電子（一般に伝導電子）の散乱を引き起こし，Curie温度以下での電気抵抗の異常な温度依存性の原因となることを示した．このモデルは現在では希土類金属によく当てはまると考えられており，そのスピン構造がよく説明される．5)

現在では鉄族遷移金属の3d電子は動き回ると考えられているが，例えばCuに少量のMnやFeを混ぜた希薄磁性合金ではMnやFeの3d電子は局在しているのは確かで，sdモデルはこの場合によく成り立つと考えられる．芳田6)は磁性不純物Mnによるsd相互作用で引き起こされる伝導電子のスピン偏極が，その不純物を中心に振動しながら R−3に比例して減少することを示し，CuMn系における電子スピン共鳴の実験7)を説明した．またMn不純物は当然Cuの電気抵抗を引き起こすが，電子の散乱はMnのポテンシャル以外にsd相互作用からも生じ，後者からくる電気抵抗は外部磁場によって減少することを芳田8)は示した．

sd相互作用と同じ型の相互作用は金属中の核スピンと伝導電子の間にもあり，RudermanとKittel9)は2次摂動で核スピン間の交換相互作用を導いている．この型の相互作用はRKKY相互作用と呼ばれている．

§3.　Anderson模型

CuMn系の実験を契機として希薄磁性合金の実験が盛んになったが，Clogston等10)の実験で，ホストの金属（Cuに相当するもので，彼らは5d遷移金属を用いた）によっては磁性不純物（彼らの場合Fe）がスピンを持たない場合のあることがわかってきた．この問題はFriedel11)がすでに考察しており，3d電子間のクーロン相互作用が関係するのであるが，Anderson12)は簡単なモデルから不純物がスピンを持つかどうかの判定規準を導いた．簡単のため不純物の3d軌道を縮退がないとし，それに2コの電子が入ると電子間にUだけのエネルギーが生じ，また4s電子は3d軌道に入ったり出たりできるとする．（その行列要素をVと書く．）もし3dスピンが上を向いていると，下向きスピンの4s電子はその3d軌道に入ってエネルギーを下げることができる．もしUが0または小さければ，3d軌道に上下同数のスピンが入ってスピンは消えるだろう．Uが大きければ下向きスピンはあまり入ることはできず，スピンは保持される．このモデルは簡単であるが問題の本質を含んでおり，多くの研究を誘発した．スピン生成の判定規準を導いたAnderson12)の取り扱いは平均場近似であり，それを越えるにはどうしたらよいかが問題点であった．

このモデルはUが大きいときsd相互作用に帰し， J がUとVから導き出される．13, 14)Uが大きいとき，Uの項を無摂動項にとり，Vの項について2次摂動を行えば，4s電子の散乱過程が得られるが，これが3dと4sのスピンの相対的な向きによるので，結局交換相互作用の形に書ける．このようにして導かれた J は負となる．このことは重要な意味を持つことになる．

§4.　電気抵抗極小

金属の電気抵抗は一般に温度が下がると減少するが，ヘリウム温度ではどのように振舞うかは，ヘリウムの液化の時より関心が持たれていた．1930年にMeissnerとVoigtはMg等の電気抵抗が4Kよりも1Kの方が大きいことを見いだした．15)ついでde Boer達は幾つかの金属の抵抗温度曲線に極小が現れるのを見いだした．16)この問題は電気抵抗極小の問題といわれ，なぜ金属の電気抵抗が温度が下がると増大するのか，どのような場合にこれが起こるのかについて，沢山の研究がなされた．その結果，これは金属が少量の磁性不純物を含む場合に起こることが分かってきた．典型例はCu, Ag, AuにFe, Mn, Coを少量いれた場合で，ppm程度の量でも起こるから，試料のコントロールが難しく実験家を悩ませた．Snのような非磁性不純物でも起きることがあり，磁性不純物は完全な定説とはなっていなかったが，Sarachik達17)の実験はこれを決定的にした．彼女はClogston達10)の試料の電気抵抗を測定し，不純物（この場合Fe）がスピンを持つか持たないかが，抵抗極小が起こるか起こらないかと完全に合致することをみた．Snの場合は，精製不十分の母体（この場合Cu）に酸化された形で含まれていたFeがSnにより還元され，Feが磁性不純物の役割をしていたものである．

実験が進むと，この現象が磁性不純物を少量含む金属ではごく一般に起こることが分かってきた．しかし再現性が悪く，システマティックな結果はほとんどなかった．不純物による電気抵抗は，不純物濃度が小さいときは濃度に比例し，ふつうは温度によらないが，磁性不純物の時はそれが温度によるということで，その温度依存性の部分が濃度に比例するかどうかについても，はっきりしたデータはほとんどなかった．このころ筆者は，Cuに磁性不純物としてFeをいれた系についてのKnookの博士論文18)をみる機会を得た．これは実にきれいなデータで，不純物濃度に比例する現象であることがはっきり分かった．つまり各不純物が独立に温度変化する抵抗に寄与していることになる．この論文からまた，電気抵抗の増大が0.1 Kのような低温でも止まらないことを知った．これはMacDonald19)達の論文にすでにはっきりと見えていたことでもある．一般にある系の特徴的な温度より実際の温度が低くなれば温度依存性はなくなるものである．このような系がどうして0.1 Kよりも小さい特性温度を持つのかが不思議であった．

この現象の理論的説明もこの点がポイントだった．磁性不純物間の相互作用が何らかの原因とすれば，0.1 Kという値もおかしくはなかったが，そうすると不純物濃度の2乗に比例することになってしまう．特殊なモデルを考えることもできなくはないが，この現象が普遍的であることは説明できなくなる．普遍的である点ではsdモデルならよいが，それによる電気抵抗は糟谷，3)芳田8)により計算されていて，温度によらなかった．

この問題は結局sdモデルをとり，電気抵抗の計算の近似を進めることによって解決した．20)sd相互作用による電子の散乱確率を最低次で計算すると J 2のオーダーになる．次の J 3次の項はlog(kT/D)に比例する項を含む．Dは4s電子のFermiエネルギー程度の量である．これは J が負のときTの減少と共に増大し，実験を説明する．実際低温になればなるほど急激に増大するという実に不思議な結果19)を説明できた． J 3の項では電子はいったん中間状態に散乱されて最終状態に散乱される．sd相互作用でなければこのとき他の電子の存在を考えなくてよい．すると単なるポテンシャルによる一体散乱に帰し，高次を考えてもなにも起こらない．sd相互作用では，ある電子がスピンを反転する散乱を行ったとすると，別の電子にとってはその反転の前に散乱したか後にするかで結果は違ってくる．つまり問題は多体問題となる．結局 J 3の項の中間状態では，他電子の存在を考慮してFermiレベルより上の状態のみを考慮するという項が現れる．0.1 Kといった小さいエネルギーの起源は4s電子の励起エネルギーであり，これは金属では0から始まって連続的に増加する．これがlog Tの項を与える．ここではFermi面という電子の占有数が不連続に飛ぶ境界のあることが本質的であり，そのことから起こる現象をFermi面効果と呼ぶ．

§5.　その後の発展

このように電気抵抗極小の説明はできたが，log TはT＝0で発散してしまう．この点に関する研究が世界的に始まった．それはまず J の更に高次の項を調べるものであった．Abrikosov21)は散乱のTマトリックスの最低次項( J 1)を1として高次項が[ J r log(e/D)]nであることを示した．eはFermiレベルから測った電子のエネルギー，rはFermiレベルにおける4s電子の状態密度である．これによると， J が負のとき温度がTKDexp(1/ J r)で***展開の各項が同じになり結果は発散してしまう．Suhl22)はChew-Lowの散乱理論を用いて閉じた結果を得たが，展開の一般項は( J r)m[ J r log(e/D)]nの形になっている．長岡23)は2時間Green関数の運動方程式を途中で近似して閉じた方程式を導き，これはHamann,24) その他25)によって解かれ，その結果はSuhlと全く同じになった．これらによると， J ＜0のとき電気抵抗は高温ではlogTに従い，TK以下で一定値に近づく．このころ実験的にもlogTが最後にどうなるかが関心が持たれており，典型物質Cu-Mnでは非常な低温が必要と思われていた．ところが久米26)はAuにVを混ぜた系で，Daybell-Steyert27)はCuにFeを混ぜた系で，logTよりはずれた電気抵抗が最後に一定値に近づくのを見いだし，それぞれTK＝300 Kおよび18 Kを得た．その表式から分かるように，TKの値は非常に小さいものから大きいものまであり得るのであった．TK以下の問題で実験家が一歩先んじた感があった．

ではT＝0で金属中の磁性不純物はどのような状態にあるのか．芳田・興地28)はその帯磁率を計算した． J ＝0なら不純物スピンは独立でCurie帯磁率c＝C/Tが得られる． J についての摂動展開でlogTを含む項が生じ， J ＜0ならCは温度が下がると減少し，Abrikosovと同じ近似でTKでCが負に発散する．またこの系の自由エネルギー，すなわち比熱またはエントロピーの計算も行われた．29, 30) J ＝0ではエントロピーはk log(2S＋1)であるが（局在スピンがSの時），高次項は J 3から始まっていて J ＜0なら負であり，やはりlogT項が現れてTKで発散する．これらの結果からはTK以下の様子を正しくいうことはできないが，TK以上でsd相互作用のために不純物スピンの自由度が押さえられる（縮退がとれる）ことが始まっていると考えてよい．

以上の取り扱いはすべて不純物スピンがdoubletの状態を出発点とした J についての摂動計算である． 芳田・興地・吉森31)は，そのような取り扱いでは J ＜0のとき正しい基底状態は得られないと考え，1個の不純物の系の基底状態を変分関数で表した．4s電子を1個取り出して不純物スピンとsingletに結合させ，他の4s電子はFermi球にとる．つぎにsd相互作用を摂動で扱って電子ホール対のできた状態を次々と取り入れてゆく．このようにして彼らは，不純物スピンがdoubletである状態を出発点として，sd相互作用を摂動で取り入れたときの基底状態のエネルギーよりも， J ＜0のときのこの基底状態のエネルギーはkTKだけ低いことを示した．

このように1個の不純物スピンの状態はTKを境にして大きく変わることになる．しかし，ある温度でなんらかの不連続な変化が起こるとは思えなかった．ということはTKより高温でスピンがdoubletであるときに正しい答えが得られれば，それには基底状態も正しく含まれていると考えなければならない．実際，doublet状態での比熱の異常項は基底エネルギーのkTKの下がりに移行すると考えられる．問題はdoublet状態での正しい答えを得ることであって，Suhl, 長岡程度のよい近似ではT→0のとき正しい基底状態に近づかず，厳密解が得られて初めてこのことが確認された．問題はそのように難しかったけれども，それ以上の問題でもなかった，ともいえる．

§6.Nozi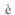res-Dominicisの時間に依存する摂動論

ちょうどこの頃に，金属のX線吸収・放出に関するMahan32)の論文が出た．電子が内殻のあるレベルからFermiレベルより上のあるレベルまで上げられると，その瞬間から内殻にホールが生じ，上げられた電子はそのポテンシャルを感じて別のレベルへ散乱される．結局あるレベルに達するまでに，散乱を0回，1回，2回…と繰り返す．その中間状態はFermiレベルより上についてだけ加えるから，そこから対数項が生ずる．電子の最終エネルギーをFermiレベルから測ってεとすれば，1回の散乱からlogeが生ずる．またFermi球を構成する電子もホールのポテンシャルを感じて散乱される．これらの効果によりX線の吸収スペクトルにeのベキに比例した項が生ずる．これもFermi面効果と言うことができる．Nozires-deDominicis33)はこの問題を時間に依存する問題に書き換えた．ある瞬間にホールが生ずると，それまでのFermi球はどう変化して行くか．またFermi面より上に置かれた電子の状態はどう変化して行くか．摂動の働く時間が有限である場合のGreen関数に対する方程式をたててこれを正しく解いた．それによると，ある瞬間にホールポテンシャルが生じた時，Fermi球を形成している電子の応答は時間のベキで表される．つまり非常に遅いということで，それは電子の励起エネルギーがゼロから始まるからである．その結果Mahanのベキ則に現われるベキには，ホールのポテンシャルによって生ずる1電子波動関数のphase shiftの，Fermiレベルにおける値が入ることになった．

この問題はsd相互作用の問題にも関係が深い．Anderson-Yuval34)はsd相互作用のうち，スピンのz成分を変えない部分(spin-non-flippart)を非摂動項にとりこみ，spin-flip partを摂動として展開した．n次の項においてnコの摂動を時間（または虚時間）の順序に並べたとき，一つの摂動から次の摂動までsd相互作用のspin-non-flip partは非摂動項として電子に働いているが，次の摂動が作用するとその符号が変わってしまって，その次の摂動まで続く．これはホールポテンシャルが有限の時間働くのと同じで，Nozires達の結果が使える．Anderson-Yuvalはこのようにして状態和のような量の展開式を導いた． Anderson, YuvalとHamann35)は，状態和に最も寄与する項ではspin-flipの摂動が虚時間軸上でどのような配列をするかを問題とした．もし二つのspin-flipが隣り合って対を作る傾向にあれば，スピンの向きはすぐに元に戻ってしまうということで，長い目で見ればスピンはある方向を向いている．もしそれがランダムに並んでいれば，スピンは絶えず向きを変えていて平均として消滅している．彼らのスケーリングの方法によると，パラメーターの値（ J , Dなど）がある方程式に従って変化するなら，それらが変化しても状態和などは同じである．これによって摂動の使えない低温の場合も高温の場合に直して考えることができ，それによると J ＜0のときはTKより低温でスピンが消滅していると結論された．しかしスケーリングの式はT＜TKでは正確でなくなってしまい，定性的な議論に留まった．

§7.　芳田・山田理論

磁性不純物のT＝0付近の振舞を調べるために，芳田・山田36)はAnderson模型から出発した．実験により J が負であるので， Anderson模型が現実に沿っていると考えるのは当然である．U＝0であれば3d軌道には上下スピンが自由に出入りしている．その速さはエネルギーで表せばDpV2rの程度であり，したがってスピンの向きもこの程度の速さで変わっている．3d電子から来る帯磁率cはmB2/D程度で，比熱はgTとなり， gはkB2/Dの程度である．Uをだんだん増加させると，Hartree近似12)ではあるところでスピンが発生しsd模型に移行する．しかし，1不純物の問題で不連続が起こるはずはないから，Uが非常に大きくてもT＝0付近では定性的にはU＝0と同じ振舞が期待される．すなわち帯磁率は有限で，比熱はTに比例し，また電気抵抗の温度変化はT 2に比例する．ところがUが非常に大きければそれはsd模型と同じことであるから，同じ振舞はsd模型のT＝0付近の振舞でもある．Suhl, 長岡ではこの振舞が得られなかった．芳田・山田は自由エネルギーをUについて展開し，一般項の正しい表式を得た．それから上記の振舞に現れる物理量の表式を得ることができた．しかしそれらを J で表すことはできないから，sd模型の立場からは定性的な結果である．しかし物理量間の関係についてはU→の時，簡単な関係が得られる．特に(c/mB2)/(g/kB2)をap2/3と書いたときに， U→でa→2であることが示された．aはWilson比といわれる大切な物理量で，U＝0ならa＝1である．

§8.　Wilsonの理論37)

ここと次の章ではハミルトニアンを取り扱い易いように簡単化することから始まる．sd相互作用をδ関数型とすれば動徑方向の1次元の問題となる．波数ベクトルの大きさkは等間隔に並んでいるが，Fermi面付近の低い励起が重要であり，すべてのkを同等に扱うのはふさわしくない．しかし高い励起も大切で，電子がスピンと相互作用するときはスピンの位置に居ることは確かだから，不確定性原理から電子は大きいエネルギーを持つ．結局スピンより遠い位置での高い励起はこの問題については重要でない．このようにしてハミルトニアンから不要な部分を取り去ってWilson37)が到達したモデルは，次のようなものである．半直線の一端に局在したスピンがあり，それに続いて原子軌道が並ぶ．軌道間の飛び移り積分は一つ隣に移る毎に1/L（Lは2から3ぐらいの適当な値にとる）になり，またスピンに隣接した軌道とスピンの間には交換相互作用が働くとする．スピンのすぐ近くで飛び移り積分が1eVであったとしても，100も進めばそれは事実上ゼロとなり，Fermi面直上の励起に対応する．原子軌道1個当り1個の電子をおく．

1022もの電子の問題を100個ほどの電子の問題で解いて正しい答えを期待するのは，この問題ではユニバーサリティが成り立つだろうという信念に基づいている．計算機により，まずスピンの近くの数個の問題をとき，それを用いて一つ隣を含めた問題を解く．これを繰り返して100個に至るのは難しくない．低い励起を取り込んでいくのは低温に向かっていくことに対応し，100個を解いたということは低温まで解いたということである．このようにしてWilsonは帯磁率，比熱を全温度領域で求めた．その結果まず，温度をTKでスケールすれば，異なる J の場合が一つの曲線に乗ることが分かった．そのことと高温での摂動展開の結果を結び付けて，低温での物理量（帯磁率，比熱のg）をTKを用いて数係数まで求めることができ，Wilson比はやはり2となった．100まで解いた時の低エネルギー励起はFermi流体論で表されるようなもので，これが低温における物理量に反映している．

§9.　厳密解

Andrei38)とWiegmann39)は独立にこの問題の厳密解を提出した．彼らはユニバーサリティを信じる立場から次のように問題を簡単化した．すなわちスピンを原点に置いた直線上を電子は右向きにのみ走り，スピンと交換相互作用を行うとした．このとき波動関数を電子達の座標の関数で表すと，各電子は平面波で表されるが，スピンを通過するとその位相が変わり，スピンの向きも一般に変化する．二つの電子がスピンの左から右へ通過したとき，どちらが先に通過したかで最後のスピン状態は異なる．したがってx1＞x2とx1＜x2とは別の領域としなければならない．N電子の時もすべての領域でスピン関数は異なるが，電子の波数は同じものを用いるという仮定 （Bethe仮説） の下で，すべての領域のスピン関数の間の関係を矛盾なく定める（Schrdinger方程式を解く）ことができた．残る1個のスピン関数を境界条件から定めるのに，1次元Heisenberg模型の厳密解を求める手法がそのまま用いられる．このようにして彼らは全温度領域で比熱，帯磁率を求めることができたが，そのためには連立積分方程式を数値的に解くことが必要なだけであった．その結果はTKでスケールすればWilsonと全く一致し，ユニバーサリティが成り立っていることが分かる．低温での帯磁率や比熱のgの数係数はp, eと一つの定積分で表されるが，Wilsonの数値計算と精度の範囲内で一致した．また彼らは絶対零度で任意の外部磁場のもとでの磁化を求めることができた．

§10.　おわりに

このようにして明らかになった金属中の磁性不純物の物理像は次のようなものである．Anderson模型でまずU＝0の場合を考えれば，4s電子は上下いずれのスピンのものも，逆スピンの電子におかまいなくDの速さで3d軌道に出入りしている．したがって3dのスピンは非常に速く(D1eV)向きを変え，非磁性と見ることができる．Uが0でないと上下スピンの動きには相関が生ずるが，UがDよりはるかに大きくなると，上向きスピンが3d軌道にいる間は下向きスピンは入ることができず，上向きスピンがいなくなって初めて入ることができる．このように3dスピンはやはり絶えず向きを変えているが，ポイントはその速さがDよりもはるかに遅くなってkTK程度になるということである．しかしいくら遅くとも絶えず向きを変えているから，絶対零度では非磁性にみえる．もしこの系が温度TにあるとkT程度のエネルギーの不確定があり，不確定性原理から，時間でいえば高々/kT程度の時間でこの系を観測することになる．すると，T＞TKになるとスピンが向きを変えるよりも短い時間で観測することになるから，スピンはどちらかを向いており磁性を持つようにみえる．

Uがあるとなぜスピンの向きが遅く変わるのかが最後のポイントであるが，これをFermi面効果と呼んでよいであろう．たとえば下向きスピンの4s電子には，上向きスピンの3d電子がいなくなった瞬間から3d軌道に飛び込む摂動が働く．するとそのあと4s電子の波動関数は時間と共に変化してゆくが，Nozires-Dominicisのところで述べたようにその変化はゆっくりであって， そのため結局3d軌道への出入りが遅くなるのである．

このようなFermi面効果のもう一つの例をあげておく．一般に縮退したFermi系にある瞬間から不純物ポテンシャルが働いたとする．その後の変化はNozires-Dominicisの示す通りであるが，十分時間のたった後到達した状態と最初の状態とは一般に直交している．これをAndersonの直交定理という．40)この定理は一般化できて，不純物ポテンシャルがある場所に働く場合の（最終的な）波動関数と，別の場所に働く時の波動関数とは一般に直交している．そうすると次のような問題が考えられる．金属の中に1個の陽子があったとしよう．これは格子間位置にいて伝導電子にポテンシャルをおよぼす．ところが陽子は核としては軽いので隣の格子間位置にトンネルすることがありうる．すると伝導電子には別の位置からポテンシャルがおよび，二つの状態の重なり積分は伝導電子に関する部分はゼロとなってしまう．このことは陽子のトンネルの行列要素が小さくなることを意味する．41)直交定理は無限の時間の後に成り立つが，陽子はトンネルした後すぐにまたトンネルしていなくなるので，ゼロにはならない．これから陽子の金属中での拡散係数が温度のベキで変化することが示される．42, 43)実験的にも正ミュオンのCu中の拡散44)や，Nb中の陽子の中性子散乱45)からこのことが見いだされている．

文　献

  1. J. Kondo and A. Yoshimori, ed.: Fermi Surface Effects (Springer, 1988). 近藤 淳：『金属電子論』（裳華房，1983）．芳田 奎：『磁性』（岩波書店，1991）．
  2. C. Zener: Phys. Rev. 81 (1951) 440.
  3. T. Kasuya: Prog. Theor. Phys. 16 (1956) 45.
  4. T. Kasuya: Prog. Theor. Phys. 16 (1956) 58.
  5. K. Yosida and A. Watabe: Prog. Theor. Phys. 28 (1962) 361.
  6. K. Yosida: Phys. Rev. 106 (1957) 893.
  7. J. Owen, M. Browne, W. D. Knight and C. Kittel: Phys. Rev. 102 (1956) 1501.
  8. K. Yosida: Phys. Rev. 107 (1957) 396.
  9. M. A. Ruderman and C. Kittel: Phys. Rev. 96 (1954) 99.
  10. A. M. Clogston, B. T. Matthias, M. Peter, H. J. Williams, E. Corenzwit and R. C. Sherwood: Phys. Rev. 125 (1962) 541.
  11. J. Friedel: Nuovo Cimento Suppl. 7 (1958) 287.
  12. P. W. Anderson: Phys. Rev. 124 (1961) 41.
  13. J. Kondo: Prog. Theor. Phys. 28 (1962) 846.
  14. J. R. Shrieffer and P. A. Wolff: Phys. Rev. 149 (1966) 491.
  15. W. Meissner and G. Voigt: Ann. Phys. (Germany) 7 (1930) 761 and 892.
  16. W. J. de Haas, J. de Boer and G. J. van den Berg: Physica 1 (1933/34) 1115.
  17. M. P. Sarachik, E. Corenzwit and L. D. Longinotti: Phys. Rev. 135 (1964) A1041.
  18. B. Knook: Thesis, Univ. of Leiden, 1962.
  19. D. K. C. MacDonald, W. B. Pearson and I. M. Templeton: Proc. Roy. Soc. 266 (1962) 161.
  20. J. Kondo: Prog. Theor. Phys. 32 (1964) 37.
  21. A. A. Abrikosov: Physics 2 (1965) 5.
  22. H. Suhl: Phys. Rev. 138 (1965) A515, 141 (1966) 483.
  23. Y. Nagaoka: Phys. Rev. 138 (1965) A1112.
  24. D. R. Hamann: Phys. Rev. 158 (1967) 570.
  25. J. Zittarz and E. M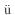ller-Hartmann: Z. Phys. 212 (1968) 380.
  26. K. Kume: J. Phys. Soc. Jpn. 23 (1967) 1226.
  27. M. D. Daybell and W. A. Steyert: Phys. Rev. Lett. 18 (1967) 398.
  28. K. Yosida and A. Okiji: Prog. Theor. Phys. 34 (1965) 505.
  29. J. Kondo: Prog. Theor. Phys. 40 (1968) 683.
  30. K. Yosida and H. Miwa: Prog. Theor. Phys. 41 (1969) 1416.
  31. K. Yosida: Phys. Rev. 147 (1966) 223, およびそれに続く論文．文献1 の芳田の著書を参照．
  32. G. D. Mahan: Phys. Rev. 163 (1967) 612.
  33. P. Nozi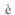res and C. T. deDominicis: Phys. Rev. 178 (1969) 1097.
  34. P. W. Anderson and G. Yuval: Phys. Rev. Lett. 23 (1969) 89. G. Yuval and P. W. Anderson: Phys. Rev. B 1 (1970) 1522.
  35. P. W. Anderson, G. Yuval and D. R. Hamann: Phys. Rev. B 1 (1970) 4464.
  36. K. Yosida and K. Yamada: Prog. Theor. Phys. Suppl. 46 (1970) 244, およびそれに続く論文．文献1の芳田の著書を参照．
  37. K. Wilson: Rev. Mod. Phys. 47 (1975) 773.
  38. N. Andrei: Phys. Rev. Lett. 45 (1980) 379. N. Andrei, K. Furuya and J. H. Lowenstein: Rev. Mod. Phys. 55 (1983) 331.
  39. P. B. Wiegmann: J. Phys. C 14 (1981) 1463. A. M. Tsvelisk and P. B. Wiegmann: Adv. Phys. 32 (1983) 453.
  40. P. W. Anderson: Phys. Rev. Lett. 18 (1967) 1049; Phys. Rev. 164 (1967) 352.
  41. J. Kondo: Physica 84B (1976) 40.
  42. J. Kondo: Physica 125B (1984) 279.
  43. K. Yamada, A. Sakurai and S. Miyazima: Prog. Theor. Phys. 73 (1985) 1342.
  44. R. Kadono, T. Matsuzaki, K. Nagamine, T. Yamazaki, D. Richter and J.-M. Welter: Hyperfine Interact. 31 (1986) 205.
  45. A. Magerl, A. J. Dianoux, H. Wipf, K. Neimaier and I. S. Anderson: Phys. Rev. Lett. 56 (1986) 159.

*168東京都杉並区上高井戸2-2-29

**編集部注：この場合のFermi面効果は一般には近藤効果と呼ばれる．

***編集部注：TKは近藤温度と呼ばれている．